Zad. 1. Przez jakie państwo przechodzi:
a) równik i południk zerowy?
b) równik i południk 180°?
c) zwrotnik Raka i południk zerowy?
d) zwrotnik Koziorożca i południk zerowy?
e) zwrotnik Raka i południk 180°?
f) zwrotnik Koziorożca i południk 180°?
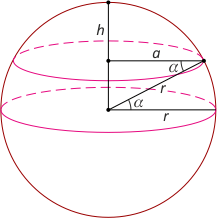
Zad. 2. Który równoleżnik odcina ćwierć objętości kuli ziemskiej?
Zad. 3. Janek mieszka w centrum Wrocławia, w 10-piętrowym bloku (ma on parter i piętra od 1 do 9). W jego klatce schodowej na każdej kondygnacji jest jedna lampa i jej włącznik. Wracając nocą do domu, kiedy wszyscy sąsiedzi już śpią, Janek zawsze gra w następującą grę: wbiega do budynku i gasi światła na kolejnych kondygnacjach, zaczynając od parteru, aż do pierwszej kondygnacji, na której światło jest zgaszone. Tam zapala światło, wybiega z budynku, patrzy na nowy układ zapalonych świateł i powtarza zabawę. Kończy ją tylko wówczas, gdy światła palą się na wszystkich piętrach. Pewnego dnia Janek wbiegał do budynku 500 razy i po wyjściu zobaczył, że światła są zapalone tylko na III, V i IX piętrze. Jaki był stan oświetlenia na IV piętrze, kiedy zaczynał zabawę?
W tym miesiącu punkty zdobyli:
- 3 - Krystyna Lisiowska - redaktor z Warszawy, Marzena Wąsiewicz - nauczycielka z Kajetan,
- 2,5 - Szymon Meyer - analityk danych z Dziewkowic,
- 2 - Oliwia Makuch - studentka matematyki na PWr, Kasper Przenzak - analityk ryzyka z Krakowa.
Zad. 1.
a) (0°, 0°) - żadne (tzw. Wyspa Null w Zatoce Gwinejskiej)
b) (0°, 180°) - terytorium morskie Kiribati na północ od Nikunau (Wyspy Gilberta)
c) (23.4394°, 0°) - Algieria
d) (-23.4394°, 0°) - żadne (Ocean Atlantycki Południowy)
e) (23.4394°, 180°) - żadne (Ocean Spokojny Północny)
f) (-23.4394°, 180°) - atole Minerva Reefs na Oceanie Spokojnym, terytorium sporne Wysp Fidżi i Tonga.
Zad. 2. Ćwierć objętości kuli odcina równoleżnik 20.32°. Przyjmijmy średni promień Ziemi r = 6371 km. Korzystamy ze wzoru na objętość odcinka kuli o promieniu r i wysokości h, tzn. V = 1/3(πh²)·(3r–h) i otrzymujemy równanie 1/4·4/3·πr3 = πh2r–π/3⋅h3 lub po przekształceniach
h3–3h2r+r3 = 0, skąd wyliczamy (np. na kalkulatorze graficznym) h = 4158,4 km. Jeśli α jest szerokością geograficzną na półkuli północnej szukanego równoleżnika, mamy sinα = (r–h)/r, skąd po podstawieniu liczb mamy sinα = 0,3473 i (na kalkulatorze naukowym) otrzymujemy α = 20,32° (stosunkowo blisko zwrotnika Raka). W obliczeniach można też wykorzystać jakiś internetowy kalkulator objętości kuli.
Zad. 3. Na początku zabawy na IV piętrze światło było zapalone. Układ zapalonych i zgaszonych świateł można interpretować jako ilustrację zapisu liczby w systemie dwójkowym, a każde wejście do budynku generuje liczbę o 1 większą niż zapalona poprzednio (dlaczego?). Na koniec zabawy Janek zauważył liczbę 23+25+29 = 552. 500 wejść wcześniej zapalona była liczba 52 = 32+16+4 = 25+24+22, czyli na IV piętrze światło było na początku zapalone.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
