Zad. 1. Jak podzielić powierzchnię szachownicy na cztery identyczne części tak, aby w każdej z nich znajdował się jeden skoczek? Linie dzielące szachownicę nie mogą przecinać pól.
Zad. 2. Antoni i Franciszek grali w pewną grę: na przemian kładli identyczne pudełka po zapałkach na kwadratowym stole o wymiarach 1m x 1m. Rozpoczął Franciszek. Jedyną zasadą było, aby następne pudełko nie dotykało żadnego z wcześniej położonych. Przegrywał ten, który nie mógł dołożyć następnego pudełka. Czy któryś z chłopców przy najlepszej grze obu zawodników może być pewny wygranej i jaką taktykę powinien zastosować?
Zad. 3. W szkole podstawowej w Łamigłówkowie nauczyciel matematyki w ramach kary za niewłaściwe zachowanie podczas lekcji zadawał uczniom dodatkowe zadania domowe. Zestawy karnych zadań znajdowały się w 12 pudełkach ustawionych w kole na biurku nauczyciela. Pewnego dnia nauczyciel kazał Jasiowi, który nie uważał podczas lekcji, podejść do biurka i powiedział:"Jedno z tych pudełek jest puste. Obok niego, w kierunku ruchu wskazówek zegara, znajduje się pudełko, w którym jest jedno zadanie. Obok, w tym samym kierunku, leży pudełko, w którym są dwa zadania i tak dalej, aż do ostatniego, w którym jest jedenaście zadań. Wybierz pudełko i jako karę za złe zachowanie podczas lekcji, rozwiąż do jutra wszystkie zadania, które w nim znajdziesz.” Sprytny Jaś, który chciał uniknąć rozwiązywania zadań, zauważył, że pudełka miały naklejone karteczki z liczbami. Licząc zgodnie z ruchem wskazówek zegara, znajdowały się na nich kolejno liczby: 0, 2, 7, 10, 1, 3, 6, 11, 8, 4, 5, 9. Jaś spytał: „W ilu przypadkach liczba na pudełku jest taka sama, jak liczba zadań, które się w nim znajdują?” Nauczyciel odpowiedział: „Gdybym ci powiedział, wiedziałbyś, które pudełko jest puste.” Jaś po chwili zastanowienia wybrał pudełko, które okazało się puste. Które to było pudełko?
Z kwietniowymi łamigłówkami uczestnicy poradzili sobie bardzo dobrze. Prawie trzy czwarte zawodników rozwiązało pierwsze dwa zadania. Najłatwiejsza okazała się ostatnia łamigłówka.Komplet 3 punktów zdobyli: Jacek Bagiński - nauczyciel matematyki z Krakowa, Kamila Bojar - uczennica Zespołu Szkół Ponadgimnazjalnych w Szprotawie, Daria Bumażnik - uczennica II LO w Jeleniej Górze, Bartosz Czyżewski - uczeń I LO w Jeleniej Górze, Andrzej Piasecki - administrator IT z Oleśnicy, Tomasz Porębski - uczeń I LO w Krakowie, Jakub Ptak - uczeń SP 64 we Wrocławiu, Tomasz Skalski - student matematyki na PWr , Sabina Sy - studentka nanotechnologii na UJ, Wojciech Tomiczek - inżynier z Lipowej, Marzena Wąsiewicz - informatyk, a obecnie gospodyni domowa z Kajetan i Piotr Wróbel - inżynier sprzedaży z Brwinowa.
W Lidze Łamigłówkowej prowadzą:
- Tomasz Porębski (21 pkt na 21 możliwych!)
- Sabina Sy (20 pkt)
- Wojciech Tomiczek (19,5 pkt)
- Marzena Wąsiewicz (19 pkt)
- Piotr Wróbel (18,5 pkt)
- Jacek Bagiński , Bartosz Czyżewski, Andrzej Piasecki, Jakub Ptak, Tomasz Skalski, Wojciech Tobiś - student automatyki i robotyki AGH w Krakowie (18 pkt)
- Krzysztof Bednarek - uczeń III LO we Wrocławiu, Tomasz Stempniak - uczeń I LO w Ostrowie Wielkopolskim (17,5 pkt)
- Krystyna Lisiowska - redaktor z Warszawy (17 pkt)
- Kamila Bojar, Daria Bumażnik (16,5 pkt).
Wszystkim serdecznie gratulujemy!
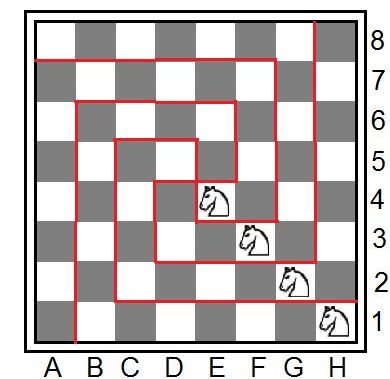
Zad. 1.
Zad. 2. Wygra Franciszek, jeśli pierwsze pudełko ustawi na środku stołu, a kolejne będzie dokładał symetrycznie względem środka stołu do pudełek ułożonych w poprzednim ruchu przez Antoniego. Jeśli Antoni dołoży swoje pudełko, to Franciszkowi na pewno też się to uda.
Zad. 3. Puste było pudełko z liczbą 7. Istnieją cztery możliwości, kiedy liczba na pudełku zgadza się z liczbą zadań w pudełku dla tylko 1 pudełka, dwie możliwości, gdy liczby te zgadzają się dla 3 pudełek i tylko jedna możliwość, gdy liczby te zgadzają się dla 2 pudełek. W ostatnim przypadku liczba zadań zgadza się z numerami na pudełkach z liczbami 3 i 9.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
