Zad.1. Finał teleturnieju "Szalone liczby" składał się z siedmiu pytań, na które należało odpowiedzieć, wpisując po kolei T (tak) lub N (nie). Oto odpowiedzi czwórki finalistów:
Anmelia: T N N N T T N
Bartosz: T N T T N T T
Cezary: N N T N T T N
Dorota: T T N T N N T
Okazało się, że jedna osoba odpowiedziała źle tylko na jedno pytanie, inna pomyliła się dwa razy, a pozostałe podały odpowiednio trzy i pięć błędnych odpowiedzi. Jaka była poprawna kolejność odpowiedzi? Kto uzyskał najlepszy wynik?
Zad.2. Jaka jest najkrótsza możliwa trasa przejścia przez wszystkie punkty a-k po liniach poniższego diagramu, rozpoczynająca się z punktu 1 i kończąca się w punkcie 2? Punkty 1 i 2 można odwiedzić dowolną liczbę razy, natomiast liczba przejść przez pozostałe punkty musi być taka sama. Odległości między dwoma sąsiednimi punktami wynoszą 1 cm, tylko odległości b-1 oraz 1-g wynoszą 2 cm.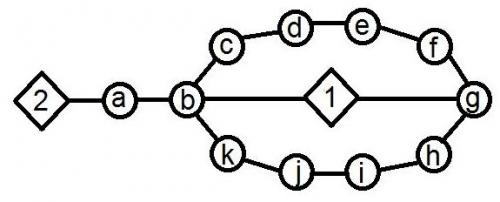 
Zad. 3. Szwajcarski bankier dał każdemu ze swoich trzech synów tyle franków, ile każdy z nich miał lat. W sumie wydał 24 franki. Następnie powiedział: „Niech najmłodszy z was połowę otrzymanych ode mnie pieniędzy zatrzyma sobie, a resztę podzieli równo między braci. Po tym podziale niech średni syn połowę posiadanych pieniędzy zostawi sobie, a resztę podzieli równo między braci. Wreszcie niech to samo zrobi najstarszy z was”. Ile lat mieli bracia, jeśli okazało się, że po zakończeniu podziałów każdy z braci otrzymał tyle samo pieniędzy?
Spośród marcowych zagadek pierwsza i trzecia nie sprawiły Łamigłówkowiczom trudności – prawie wszyscy podali bezbłędne odpowiedzi. Najtrudniejsza okazała się druga łamigłówka, którą poprawnie rozwiązała niecała połowa uczestników. Wiele osób nie zauważyło, że odległości b-1 oraz 1-g wynoszą 2 cm lub że punkty 1 i 2 można odwiedzić dowolną liczbę razy. Jako odpowiedź akceptowaliśmy podanie kolejności punktów lub długości trasy. Za wytyczenie najkrótszej trasy, ale błędne wyliczenie jej długości, przyznawaliśmy 0,5 pkt. Poprawne było także rozwiązanie, w którym przyjęto, że przejście przez punkt oznacza dojście do niego po innej linii niż zejście. W takim przypadku najkrótsza trasa miała 41 cm.
Komplet 3 punktów zdobyli: Krzysztof Danielak - uczeń I LO w Jeleniej Górze, Karolina Kamińska - uczennica OSM we Wrocławiu, Marcin Kucharski - uczeń LO w Lubaniu, Andrzej Piasecki - administrator IT z Oleśnicy, Tomasz Porębski - uczeń I LO w Krakowie, Tomasz Stempniak - uczeń I LO w Ostrowie Wielkopolskim i Marta Włóczyk - uczennica Ogólnokształcącej Szkoły Sztuk Pięknych w Opolu.
W Lidze Łamigłówkowej prowadzą:
- Tomasz Porębski (18 pkt na 18 możliwych!)
- Sabina Sy - studentka nanotechnologii na UJ (17 pkt)
- Wojciech Tomiczek - inżynier z Lipowej (16,5 pkt)
- Krystyna Lisiowska - redaktor z Warszawy, Tomasz Stempniak, Jakub Tasiemski - uczeń I LO w Krakowie, Wojciech Tobiś - student automatyki i robotyki AGH w Krakowie, Marzena Wąsiewicz - informatyk, a obecnie gospodyni domowa z Kajetan (16 pkt)
- Krzysztof Bednarek - uczeń III LO we Wrocławiu i Piotr Wróbel - inżynier sprzedaży z Brwinowa (15,5 pkt)
- Jacek Bagiński - nauczyciel matematyki z Krakowa, Bartosz Czyżewski - uczeń I LO w Jeleniej Górze, Andrzej Piasecki, Jakub Ptak - uczeń SP 64 we Wrocławiu i Tomasz Skalski - student matematyki na PWr (15 pkt).
Wszystkim serdecznie gratulujemy!
Zad. 1. TNNTNTT, najlepszy wynik uzyskał Bartosz.
Zad. 2. Najkrótsza trasa ma 25 cm, np: 1-g-f-e-d-c-b-c-d-e-f-g-h-i-h-i-j-k-j-k-b-a-2-a-2.
Zad. 3. W wyniku podziałów każdy z braci otrzymał 8 franków.Zanim najstarszy podzielił połowę swoich pieniędzy, miał 16 franków, średni i najmłodszy po 4 franki. Zanim średni podzielił połowę swoich pieniędzy, miał 8 franków, najstarszy miał 14 franków, a najmłodszy 2 franki. Zanim najmłodszy podzielił połowę swoich pieniędzy, miał 4 franki, średni miał 7 franków, a najstarszy 13 franków. Synowie Szwajcara mieli więc 4, 7 i 13 lat.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
