Strona główna › LIGA ZADANIOWA › Młodzicy (4-6 SP) › rok szkolny 2020/21

styczeń 2021

Data ostatniej modyfikacji:
2021-08-12

Zad. 1. Joasia i Bartek kupili w tym samym sklepie batony i lizaki. Za 5 batonów i 4 lizaki Bartek zapłacił 19 zł, a za 4 batony i 5 lizaków Joasia zapłaciła 17 zł. Ile kosztował baton, a ile lizak?

Zad. 2. W samochodowym Rajdzie Mistrzów startowało 14 zawodników. Organizator przyznał nagrody wszystkim uczestnikom. Każdy otrzymał o 50 euro mniej niż ten, który bezpośrednio go wyprzedził, a ostatni dostał 100 euro. Jaka była suma nagród, jeżeli na mecie nie było remisów?

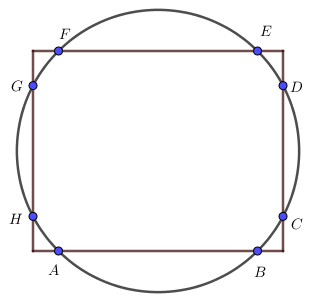
Zad. 3. Pewnego razu prostokąt powiedział do okręgu: Niestety, nie możemy mieć więcej niż n punktów wpólnych, nawet gdybyś się nadął lub skurczył. Ile wynosi n?

 

Wyniki: 

W styczniu punkty zdobyli:

  • 3 pkt. – Maria Bochenek SP Mieroszów, Ryszard Bogacz SP Smolec, Natalia Czurejno SP Wykroty, Mateusz Galik SP Arka Wrocław, Mirosław Gruszczyński SP 9 Gliwice, Maciej Hryniewicz SP 9 Gliwice, Aurelia Karpińska SP 187 Warszawa, Matylda Karpińska SP 187 Warszawa, Wiktor Kuczaj SP 7 Nowa Ruda, Julia Kubeczko SP Studzienice, Aleksander Masztalski SP 3 Mikołów, Joanna Nowakowska SP 3 Głogów, Bartosz Pawlaczyk SP 107 Wrocław, Wiktoria Pietrzak SP 3 Głogów, Maciej Pisowacki SP Mieroszów, Adrian Pokrzywa SP Nowa Wieś, Gabriel Przewoźnik SP Góra, Oliwia Raszewska SP 6 Boguszów-Gorce, Oliwia Stańczyk SP Aslan w Głogów, Wiktor Szwarczyński SP Mieroszów, Kacper Wereszczyński PSP Mieroszów, Dominika Wojdacz SP 11 Inowrocław, Anastasiia Yakovleva SP 3 Mogilno; 
  • 2 pkt. – Oktawia Budzeń SP Szkoła z Pasją Ostrowiec Świętokrzyski, Franciszek Czaplewski SP 11 Inowrocław, Maksym Osak Katolicka SP Cieszyn, Miłosz Popowicz SP 91 Wrocław, Ignacy Włodarski SP 36 Wrocław, Antoni Wójcik SP Trzebownisko, Tomasz Zawadzki SP Wodzisław; 
  • 1 pkt. – Kevin Charchut SP Iwierzyce, Michał Gatlik SP Skawinki, Zofia Prygiel SP Jedlnia Letnisko, Maria Warachim SP 24 Wocław. 

Pozostali uczestnicy otrzymali poniżej 1 punktu.

 

Odpowiedzi: 

Zad. 1. Na podstawie treści zadania stwierdzamy, że za 9 batonów i 9 lizaków Joasia i Bartek zapłacili 19+17=36 zł, a stąd wiemy, że 1 baton i 1 lizak kosztują 4 zł, a 4 batony i 4 lizaki 16 zł. Baton kosztuje, więc 19-6=3 zł, a lizak 17-16=1 zł.

Zad. 2. Najlepszy uczestnik wyścigu otrzymał 100 + 13 . 50 = 750 euro. Łączna suma nagród wynosi 750 + 700 + 650 + … + 150 + 100 = (750 + 100) + (700 + 150) + (650 + 200) + (600 + 250) + (550 + 300) + (500 + 350) + ( 450 + 400) = 7 . 850 = 5 950 euro.

Zad. 3. Okrąg może przecinać każdy bok prostokąta co najwyżej w dwóch punktach. Zatem n=8.

‹ luty 2021w góręgrudzień 2020 ›

Konkurs

Rodzic (niezweryfikowany), wtorek, 09/02/2021 - 00:04

Szanowna redakcjo! Podajecie Państwo niespójne z treścią rozwiązania zadań, już po raz drugi. Uwagi do zadania nr 3. Prostokąt, to czworokąt, który ma wszystkie kąty proste. Czworokąt jest wielokątem, który ogranicza część płaszczyzny łamaną zwyczajną zamkniętą razem z tą łamaną. Rozwiązanie, które Państwo podajecie, dotyczy wyłącznie brzegu tego prostokąta, a nie prostokąta. W zadaniu wyraźnie jest powiedziane, że to prostokąt powiedział do okręgu, a nie jego brzeg. Tak więc prostokąt z okręgiem może mieć nieskończenie wiele punktów wspólnych, a nie co najwyżej 8. Mam nadzieję, że jesteście Państwo w stanie rozróżnić koło od okręgu. Moje zadanie dla szanownej redakcji: Ile punktów wspólnych ma prostokąt z kołem? Trzymam kciuki za rozwiązanie tego zadania.

Uwaga

Mariusz Czurejno (niezweryfikowany), sobota, 13/02/2021 - 11:18

Córka odpowiedziała podobnie jak redakcja, ale po analizie powyższego komentarza sądzimy, iż była to błędna odpowiedź. Dzięki za zwrócenie uwagi na subtelną, ale znaczącą różnicę.

Powrót na górę strony