maj 2016

maj 2016

Data ostatniej modyfikacji:
2016-06-4

Zad. 1. Jakie cyfry należy wstawić za x i y, aby prawdziwy był poniższy zapis?

maj16

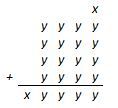
Zad. 2. Jeśli jogurt kosztuje 6 zł, batonik 9 zł, lemoniada 15 zł, a olej słonecznikowy 21 zł, to ile kosztuje czekolada?

Zad. 3. Drewniany prostopadłościan, którego wymiary wyrażone w centymetrach są liczbami naturalnymi, pomalowano zieloną farbą, a następnie rozcięto na sześciany o objętości 1 cm³ każdy. Otrzymano 8 sześcianów z trzema ściankami pomalowanymi na zielono, pewną liczbę z dwoma ściankami zielonymi, pewną liczbę z jedną ścianką zieloną i pewną liczbę sześcianów, które w ogóle nie były pomalowane.
Okazało się, że sześcianów w jakikolwiek sposób pomalowanych jest tyle samo, ile jest sześcianów niepomalowanych. Wiadomo, że ten prostopadłościan ma najmniejsze pole powierzchni całkowitej ze wszystkich prostopadłościanów o tej własności. Jakie wymiary miał prostopadłościan przed rozcięciem na sześciany?

Wyniki:

Majowe zadania okazały się niezbyt trudne - wszyscy uczestnicy rozwiązali przynajmniej dwie łamigłówki, a ponad połowa uzyskała 3 punkty. Poprawną odpowiedź do zadania 1 podali wszyscy Łamigłówkowicze.

Komplet 3 punktów zdobyli: Jacek Bagiński - nauczyciel matematyki w I LO w Krakowie, Daria Bumażnik - uczennica II LO w Jeleniej Górze, Antoni Buraczewski - uczeń SP 107 we Wrocławiu, Bartosz Czyżewski - uczeń I LO w Jeleniej Górze, Michał Kępiński - uczeń SLO w Żarach, Dawid Kubicki - student informatyki na UJ, Łukasz Jurasz - uczeń technikum ZSM-E w Żywcu, Piotr Mazur - urzędnik ze Złotoryi, Andrzej Piasecki - administrator IT z Oleśnicy, Jarosław Rybczyński - pracownik naukowy UŚ, Adrian Szumski - konstruktor z Płocka, Wojciech Tomiczek - inżynier z Lipowej, Marzena Wąsiewicz - informatyk a obecnie gospodyni domowa z Kajetan.

W Lidze Łamigłówkowej po ośmiu miesiącach prowadzą:

Antoni Buraczewski, Dawid Kubicki, Wojciech Tomiczek (23 pkt na 24 możliwe)
Michał Kępiński, Piotr Mazur, Andrzej Piasecki, Jarosław Rybczyński, Tomasz Stempniak - uczeń I LO w Ostrowie Wielkopolskim (22 pkt)
Jacek Bagiński, Aleksandra Domagała - uczennica Gim nr 23 we Wrocławiu, Krystyna Lisiowska - redaktor z Warszawy, Marzena Wąsiewicz (21 pkt)
Bartosz Czyżewski, Adrian Szumski (20,5 pkt)
Daria Bumażnik (20 pkt)
Marcin Kucharski - student matematyki na PWr, Łukasz Jurasz (19 pkt)
Arnika Piasecka - architekt, a obecnie pracownik samorządowy z Wrocławia, Franciszek Jan Stepek - uczeń Społecznego Gim w Żarach (18 pkt)
Krzysztof Bednarek - uczeń III LO we Wrocławiu, Adam Stachelek - uczeń SP 301 w Warszawie (17 pkt).

Wszystkim serdecznie gratulujemy!

Odpowiedzi:

Zad. 1. x=1, y=3 lub x=2, y=6 lub x=3, y=9.

Zad . 2. Czekolada kosztuje 12 zł. Cenę ustala liczba samogłosek wystepujących w nazwie przedmiotu. Każda samogłoska kosztuje 3 zł.

Zad. 3. Prostopadłościan miał wymiary 8 cm x 10 cm x 12 cm. Oznaczmy wymiary prostopadłościanu przez a, b, c, które to liczby są związane równaniem (a-2)(b -2)(c-2) = ¹/₂ abc. Jest ono spełnione przez następujące trójki liczb naturalnych: (5, 13, 132), (5, 14, 72), (5, 16, 42), (5, 17, 36), (5, 18, 32), (5, 20, 27), (5, 22, 24), (6, 9, 56), (6, 10, 32), (6, 11, 24), (6, 12, 20), (6, 14, 16), (7, 7, 100), (7, 8, 30), (7, 9, 20), (7, 10, 16), (8, 8, 18), (8, 9, 14), (8, 10, 12). Z prostopadłościanów o takich wymiarach ostatni ma najmniejsze pole powierzchni. Zamiast rozwiązywać skomplikowane równanie można było poszukać prostopadłościanu o wymiarach zbliżonych do sześcianu. Najmniejsze sześciany, których połowa objętości jest w przybliżeniu równa objętości sześcianu o krawędzi o 2 cm mniejszej, mają krawędzie równe 8 cm lub 10 cm.