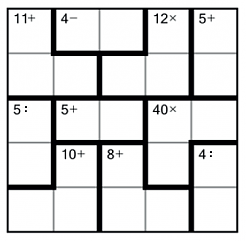
Zad. 1. Diagram poniżej przedstawia kwadrat mozaikowy. W każde jego pole należy wpisać cyfry od 1 do 5, tak żeby wszystkie wystąpiły w każdym wierszu i w każdej kolumnie. Ponadto na liczbach wpisanych w obszarach obwiedzionych grubą linią po wykonaniu wskazanego w danym obszarze działania powinien wyjść wskazany w nim wynik. W odpowiedzi podaj zawartość kolejnych wierszy diagramu.
Zad. 2. Rozwiąż zadanie logiczne (tzw. zadalog).
Pan Zdzisław postanowił usmażyć dżemy z owoców, które w dużej ilości pozostały mu po imprezie imieninowej, w tym z ogromnego ananasa. Umieścił je w słoikach po zużytych wcześniej przetworach, w tym w słoiku po korniszonach. Słoiki miały różne pojemności: 0,2 l, 0,3 l, 0,7 l, pół litra i litr, a jeden z nich miał zieloną pokrywkę. Dżem pomarańczowy miał albo czerwoną, albo żółtą pokrywkę. Słoik z dżemem mandarynkowym miał objętość o 0,3 l większą od słoika ze śliwką na etykiecie. Trzy słoiki o kolejnych coraz większych pojemnościach to ten z czerwoną pokrywką, z dżemem morelowym oraz z cukinią na etykiecie. Trzy kolejne słoiki o coraz mniejszych pojemnościach to ten z białą pokrywką, z dżemem bananowym oraz z dżemem mandarynkowym. Albo słoik z cukinią na etykiecie ma białą pokrywkę, albo ten z dżemem bananowym ma niebieską pokrywkę. Słoik z żółtą pokrywką jest większy od tego z grzybami na etykiecie. Słoik z dżemem ananasowym nie ma etykiety z papryką. Który z dżemów lekko trącił octem po korniszonach?
Zad. 3. O moich dzieciach wiadomo, że:
a) wszyscy moi synowie są szczupli,
b) wszystkie moje zdrowe dzieci uprawiają sport,
c) żadne moje dziecko, które jest łakomczuchem, nie jest szczupłe,
d) żadna moja córka nie uprawia sportu.
Czy z tego wynika, że żadne moje zdrowe dziecko nie jest łakomczuchem? Odpowiedź uzasadnij.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Jacek Bagiński - nauczyciel z Krakowa, Katarzyna Bęben I LO Kraków, Bogusz Boliński I LO Kraków, Patryk Boruń ZSP nr 2 Wałbrzych, Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr, Krzysztof Danielak - student data science na UE Wrocław, Filip Derejski I LO Kraków, Jan German - nauczyciel języków klasycznych w I LO Kraków, Andrzej Gondek I LO Kraków, Weronika Kiniorska SP 65 Wrocław, Agnieszka Klich - informatyk z Wrocławia, Jagoda Kurosad I LO Kraków, Dominika Kwaśny I LO Kraków, Krystyna Lisiowska - redaktor z Warszawy, Michał Malik I LO Kraków, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Wojciech Mura - student matematyki na UJ, Wiktoria Papiz I LO Kraków, Andrzej Piasecki - administrator IT z Oleśnicy, Tomasz Smołka I LO Kraków, Emilia Stadnicka I LO Kraków, Adrian Szumski - inżynier mechanik z Płocka, Tomasz Tomiczek - nauczyciel z Lipowej, Weronika Tracz SP Stare Bogaczowice, Michał Węgrzyn ALO PWr Wrocław, Igor Wojtun I LO Głogów,
- 2,75 pkt. - Michał Kuta I LO Kraków,
- 2 pkt. - Dominik Zygmunt - ekonomista z Białej Rawskiej.
Zad. 1. Przez nieuwagę powtórzyło się zadanie z ubiegłego roku. Przepraszamy. Wpisywane liczby czytane wierszami to: 41532, 25413, 12345, 53124, 34251.
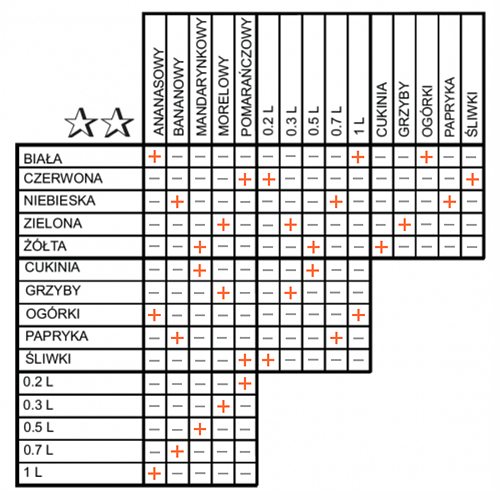
Zad. 2. Zadalogi najłatwiej rozwiązać z użyciem tzw. kartezjańskiej tabeli cech. W tym wypadku wygląda ona jak ta poniżej. Ważne jest, aby poprawnie zaklasyfikować cechy do grup i poprawnie wykonać tabelę tak, aby każda cecha krzyżowała się kartezjańsko z każdą inną i żadna cecha nie krzyżowała się sama ze sobą. W typowych pismach szaradziarskich takie tabele są na ogół gotowe, a to jest jeden z trudniejszych elementów rozwiązania. Dalej jest już prosto. Wypełniając systematycznie tabelę na podstawie informacji z zadania (np. wstawiając w poszczególne pola znaki + i -), korzystając z tego, że w każdej kolumnie i w każdym wierszu każdego wyznaczonego kwadratowego obszaru tabeli może stać tylko jeden znak +, dochodzimy do wniosku, że... korniszonami trącił dżem ananasowy.
Zad. 3. Jest to znana łamigłówka autorstwa angielskiego matematyka, profesora Uniwersytetu w Oksfordzie Charlesa Lutwidge'a Dodgsona, bardziej znanego pod swoim literackim pseudonimem - Lewis Carroll (autor "Alicji w Krainie Czarów"). Wypiszmy przesłanki, jakie podane są w treści zadania w postaci implikacji (symbol ~oznacza negację zdania).
a) SYN → SZCZUPŁY
b) ZDROWY → SPORT
c) ŁAKOMY → ~SZCZUPŁY, co jest równoważne implikacji SZCZUPŁY → ~ŁAKOMY
d) ~SYN → ~SPORT, co jest równoważne implikacji SPORT → SYN
Teraz przeprowadzamy rozumowanie dedukcyjne:
ZDROWY → SPORT (z b) → SYN (z d) → SZCZUPŁY (z a) → ~ŁAK (z c), a to właśnie należało wykazać.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
