Zad. 1. Kalkulator prosty podaje jako wartość 514 liczbę 6103515625. Oblicz sprytnie sumę 50+51+52+53+54+55+56+57+58+59+510+511+512+513. Zapisz tricki rachunkowe, z jakich korzystasz.
Uwaga! Technika sprytnych rachunków polega na wykonywaniu skomplikowanych czasem obliczeń bez używania kalkulatora ani formuł matematycznych (np. wzorów na sumę ciągu geometrycznego), z wykorzystaniem tylko podstawowych praw arytmetyki, w tym własnosci działań arytmetycznych.
Zad. 2. Trzech braci: Prawdomówny, Kłamczuch i Niezdecydowany odpowiadają na pytania TAK lub NIE. Prawdomówny zawsze mówi prawdę, Kłamczuch zawsze kłamie, a Niezdecydowany czasem mówi prawdę, a czasem kłamie (i niekoniecznie robi to naprzemiennie). Jak za pomocą trzech pytań określić, który z braci to który? Każde pytanie może być skierowane tylko do jednego z braci.
Zad. 3. Czy istnieje wielościan o 333 ścianach, z których każda jest trójkątem? Odpowiedź uzasadnij.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Jacek Bagiński - nauczyciel z Krakowa, Katarzyna Bęben I LO Kraków, Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr, Krzysztof Danielak - student data science na UE Wrocław, Andrzej Piasecki - administrator IT z Oleśnicy, Tomasz Tomiczek - nauczyciel z Lipowej,
- 2,75 pkt. - Piotr Mazur - specjalista systemów ERP ze Złotoryi, Adrian Szumski - inżynier mechanik z Płocka,
- 2,5 pkt. - Krystyna Lisiowska - redaktor z Warszawy,
- 2,25 pkt. - Bogusz Boliński I LO Kraków, Agnieszka Klich - informatyk z Wrocławia, Emilia Stadnicka I LO Kraków,
- 2 pkt. - Jan German - nauczyciel języków klasycznych w I LO Kraków, Andrzej Gondek I LO Kraków, Jagoda Kurosad I LO Kraków, Wojciech Mura - student matematyki na UJ, Michał Węgrzyn ALO PWr, Igor Wojtun I LO Głogów, Dominik Zygmunt - ekonomista z Białej Rawskiej,
- 1,5 pkt. - Weronika Tracz SP Stare Bogaczowice,
- 1,25 pkt. - Filip Derejski I LO Kraków, Wiktoria Papiz I LO Kraków
- 1 pkt. - Weronika Kiniorska SP 65 Wrocław, Tomasz Smołka I LO Kraków,
Pozostali zawodnicy za swoje rozwiązania nie otrzymali punktów.
Zad. 1. Techniki sprytnych rachunków, to taki sposób wykonywania obliczeń w pamięci, w którym wykorzystując prawa działań i inne własności arytmetyczne, zamieniamy skomplikowane rachunki na proste i łatwe do wykonania w pamięci. Do takich technik należy np.
- zamienianie mnożenia przez 5 na dopisanie zera i połowienie, 17·5 = 170:2 = 50+35 = 85
- zamienianie mnożenia przez 9 na dopisanie zera i odejmowanie, np. 17·9 = 170–17 = 153
- mnożenie lub dzielenie dużych liczb, korzystając z prawa rozdzielności mnożenia/dzielenia względem dodawania/odejmowania, np. 99·3 = 100·3 – 1·3 = 297
- zamienianie mnożenia na podwajanie i ew. dodawanie lub odejmowanie, np. 41·3 = 41·2+41 = 82+41 = 123 lub 41·7 = 41·2·2·2–41 = 328–41 = 287
- i wiele innych.
W rozwiązaniu zadania można było zastosować wiele z ww technik.
Mozna było też chytrze zastosować zapis w systemach pozycyjnych, bowiem 50+51+52+53+54+55+56+57+58+59+510+511+512+513 = 11111111111115 = 1/4 · 44444444444445 = 1/4·(514–1) = 6103515624:4 = 3051757812:2 = 1525878906.
Można było postąpić jeszcze inaczej. Oznaczmy przez x sumę 50+51+52+53+54+55+56+57+58+59+510+511+512+513. Wówczas
5x = 51+52+53+54+55+56+57+58+59+510+511+512+513+514.
Otrzymujemy równanie 5x = x–1+514, skąd 4x = 6103515624, czyli x = 1525878906.
Zad. 2. Należało zwrócić uwagę, że każde pytanie mogło być skierowane tylko do jednego z braci! Oto jedno z możliwych rozwiązań. Ustawiamy braci w pewnej kolejności i pytanie 1. kierujemy do osoby I:
1) Czy odpowiedziałbyś TAK na pytanie: Czy osoba II to Niezdecydowany?
a) odp. TAK: osoba III nie może być Niezdecydowanym (jest Prawdomównym lub Kłamczuchem), bo:
jeśli I jest Prawdomówny, to III jest Kłamczuchem,
jeśli I jest Kłamczuchem, to III jest Prawdomówny,
jesli I jest Niezdecydowany, to III nim nie jest.
b) odp. NIE: osoba II nie może być Niezdecydowanym (jest Prawdomównym lub Kłamczuchem), bo:
jeśli I jest Prawdomówny, to II jest Kłamczuchem,
jeśli I jest Kłamczuchem, to II jest Prawdomówny,
jeśli I jest Niezdecydowany, to II nim nie jest.
Pytanie 2. kierujemy w zależności od odpowiedzi napytanie I do osoby: a) III lub b) II:
2) Czy 2+2=4?
a) odp. TAK: pytany jest Prawdomówny.
b) odp. NIE: pytany jest Kłamczuchem.
Pytanie 3. kierujemy do tej samej osoby, co poprzednio (wiemy już, czy jest ona Prawdomównym, czy Kłamczuchem):
3) Czy osoba I to Niezdecydowany?
W odpowiedzi odkrywany tożsamość osoby I oraz pozostałej, jeszcze niezidentyfikowanej.
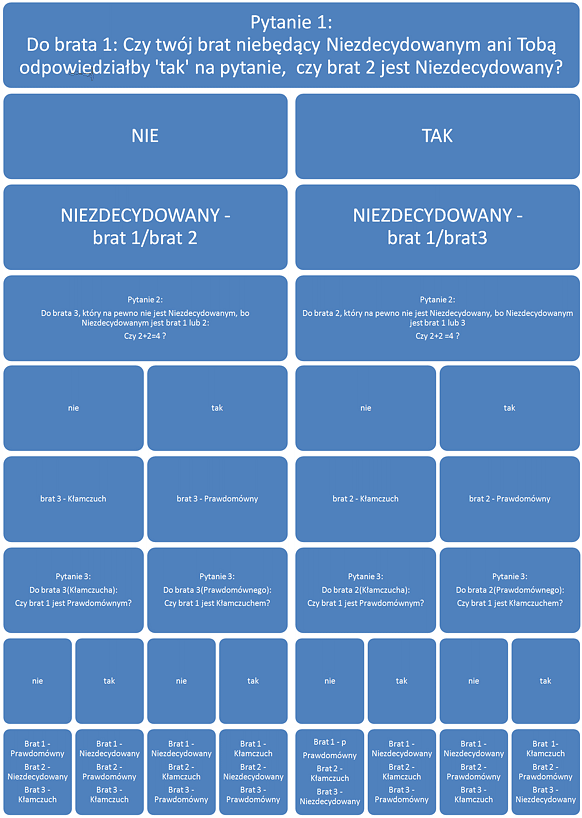
Oto inny wariant rozwiązania podany przez jednego z zawodników (kliknij, aby powiększyć).
Zad. 3. Żaden wielościan o trójkątnych ścianach nie może mieć ich 333. Wówczas liczba wszystkich boków trójkątów wynosiłaby 333·3 = 999, ale 2 boki trójkątów muszą być sklejone, żeby utworzyły krawędź wielościanu, więc liczba krawędzi to 999:2, a to nie jest liczba całkowita. Wielościan nie może mieć niecałkowitej liczby krawędzi.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
