październik 2017

październik 2017

Data ostatniej modyfikacji:
2018-07-26

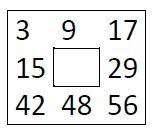
Zad. 1. Jaką liczbę należy wpisać w puste pole tabeli?

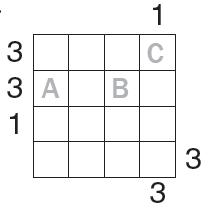
Zad. 2. Na planie osiedla ustaw wieżowce o wysokościach od 1 do 4, tak aby w każdym rzędzie i kolumnie wszystkie wieżowce miały inne wysokości. Liczby na zewnątrz tabeli wskazują, ile wieżowców widać z miejsca, w którym dana liczba stoi (wieżowce wyższe zasłaniają niższe). W odpowiedzi podaj kolejno liczby stojące w polach oznaczonych A, B, C.

Zad. 3. Przełóż jedną zapałkę tak, aby powstała równość prawdziwa.

Wyniki:

Punkty za rozwiązania zadań październikowych zdobyli:

3 pkt. - Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr, Kosma Kasprzak XXXVIII LO Poznań, Małgorzata Konarska - nauczycielka matematyki z Ostrzeszowa, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - informatyk ze Złotoryi, Igor Olszewski, SP Żórawina, Andrzej Piasecki - administrator IT z Oleśnicy, Marzena Wąsiewicz - gospodyni domowa z Kajetan, Malwina Witek SP Żórawina,
2,75 pkt. - Radosław Przekop ???,
2,5 pkt. - Bartłomiej Bąk SP Żórawina, Pataki Moneg ???, Natalia Olasz SP Żórawina, Karolina Salikow SP Żórawina, Adrian Stasiak SP Żórawina, Victoria Zarzycka SP Żórawina,
2 pkt. - Anna Magierewicz ZSP Lubań,
1,5 pkt. Miłosz Cichuta GM 1 Wrocław,
1 pkt. - Alicja Maziak SP Żórawina.

Odpowiedzi:

Zad. 1. Szukana liczba to 21.

Zad. 2. W treści zadania pojawiła się oczywista sprzeczność: cztery wieżowce o trzech różnych wysokościach. Zawodnicy przyjmowali na ogół umowną czwartą wysokość. W rozwiązaniu przyjęto, że wysokości wynoszą 1, 2, 3 lub 4. W polach A, B, C należy wówczas wstawić 1, 4, 4.

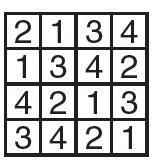
Zad. 3. Rozwiązanie przedstawia rysunek. Można przestawić zapałkę z równości do znaku minus.

Dodaj komentarz

Treść zadania 2

Anonimowy (niezweryfikowany), wtorek, 16/01/2018 - 21:02

W zadaniu drugim w każdym rzędzie mają stać 4 wieżowce, natomiast mamy tylko 3: o wysokości 1, 2 i 3. Czy na niektórych polach nie ma stać żaden wieżowiec? Jeśli tak, to czy traktować to pole jako widoczne?