Zad. 1. Jakie zwierzę skacze wyżej niż budynek 10-piętrowy?
Zad. 2. Paweł i Gaweł są bliźniakami. Paweł twierdzi, że przyszedł na świat przed Gawłem, a jednak jego urodziny przypadają dzień później niż urodziny Gawła. Jak to możliwe?
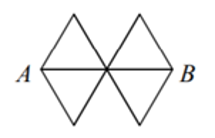
Zad. 3. Biedronka wychodzi z punktu A i spaceruje po krawędziach grafu przedstawionego na rysunku. Po żadnym odcinku nie może przejść dwukrotnie, ale może przejść przez ten sam punkt więcej niż raz. Jej wędrówka kończy się, gdy po raz pierwszy dotrze do punktu B. Na ile różnych sposobów może dostać się z punktu A do B?
W tym miesiącu punkty otrzymali:
- 3 pkt. - Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Krystyna Lisiowska - redaktor z Warszawy, Szymon Meyer - student matematyki na UWr, Adrianna Tokarska - programistka z Krakowa, Gabriela Wołynko I LO Węgrów,
- 2,75 pkt. - Tomasz Tomiczek - nauczyciel z Lipowej,
- 2,5 pkt. - Michał Węgrzyn SP 9 Wrocław,
- 2 pkt. - Krzysztof Danielak - student automatyki i robotyki na PWr, Agnieszka Klich - informatyk z Wrocławia, Janusz Szopka - informatyk z Wrocławia, Dominik Zygmunt - student bankowości i finansów cyfrowych na UŁ,
- 1 pkt. - Andrzej Piasecki - administrator IT z Oleśnicy
Zad. 1. Każde, które skacze, bowiem budynki nie skaczą.
Zad. 2. Chłopcy przyszli na świat podczas podróży z zachodu na wschód. Między urodzeniem jednego i drugiego chłopca ten środek lokomocji przekroczył linię zmiany daty (jeśli podróżowali samolotem lub statkiem) albo granicę stref czasowych (np. z godz. 0:10 na 23:10). Wówczas ten z chłopców, który urodził się później, miał datę urodzin o dzień wcześniejszą niż jego starszy brat.
Zad. 3. Jest 27 dróg z A do B. Oznaczmy przez X środkowe skrzyżowanie. Przechodzi przez nie każda droga z A do B. Ostateczny wynik to iloczyn liczby dróg z A do X oraz z B do X. Z A do X bezpośrednio można przejść na 3 sposoby i jeszcze trzeba doliczyć drogi z A do X, które przez punkt X przechodzą dwa razy. Razem jest ich 9 = 3+3·2. Dróg z X do B jest 3, bo nie można dwa razy przechodzić przez punkt B. Zatem wszystkich dróg jest 9·3=27.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
