luty 2018

luty 2018

Data ostatniej modyfikacji:
2018-09-17

Zad.1. Obwód trójkąta wynosi 18 cm. Jaka jest długość każdego z boków, jeżeli są to liczby naturalne i suma dwóch z nich jest o 6 większa od trzeciej?

Zad.2. Czy istnieje taka liczba naturalna, której iloczyn cyfr jest równy 997920?

Zad.3. Ania pojechała z rodzicami pociągiem na ferie do Kołobrzegu. Po przejechaniu połowy drogi zasnęła. Spała tak długo, że gdy się obudziła, miała jeszcze do przejechania połowę drogi, którą przespała. Jaką część drogi przespała?

Wyniki:

W lutym punkty zdobyli:

3 pkt. – Igor Wojtasik SP 11 Jelenia Góra, Paulina Hołodniuk SP 2 Wołów, Justyna Kładoczna SP 118 Wrocław, Michał Węgrzyn SP 9 Wrocław, Michał Dźwigaj SP 1 Przemków, Urszula Wąsiewicz SP Kostowiec, Antoni Adamus SP 4 Warszawa, Adam Chowanek SP Mieroszów, Michał Plata SP 2 Syców, Miłosz Zakrzewski SP Gostycyn;
2 pkt. – Patryk Buliński DSP 1 Warszawa, Wiktoria Jaguszczak SP Grębocice, Wojciech Domin SP Pisarzowice;
1 pkt. – Anna Mędrzak SP 4 Warszawa.

Pozostali uczestnicy otrzymali poniżej 1 punktu.

Odpowiedzi:

Zad. 1. Oznaczmy przez a, b i c długości boków trójkąta. Z warunków zadania mamy a+b+c = 18 i a+b = c+6. Stąd wynika, że c=6. Na podstawie nierówności trójkąta wiadomo, że w każdym trójkącie
a+b > c, a+c > b i b+c > a.
Warunek a+b > c jest spełniony wobec równości a+b = c+6.

a	1	2	3	4	5	6
b	11	10	9	8	7	6
c	6	6	6	6	6	6

Warunki zadania spełniają trójki liczb: (4, 8, 6), (5, 7, 6), (6, 6, 6).

Zad. 2. Rozkładamy liczbę 997920 na czynniki pierwsze. Ponieważ 997920 = 2⁵·3⁴·5·7·11 i jeden z czynników wynosi 11, nie istnieje liczba naturalna spełniająca warunki zadania.

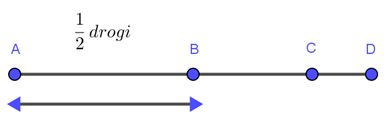
Zad. 3. Niech BC to część drogi, którą Ania przespała.
Mamy |AB| = |BD| = ¹/₂|AD| oraz |BC|+|DC| = |BC| + ¹/₂|BC| = ¹/₂|AD|.
Stąd ³/₂|BC| = ¹/₂|AD|, czyli |BC| = ¹/₃|AD|.