Zad. 1. W worku Mikołaja znajduje się pewna liczba prezentów. Jeśli Mikołaj na chybił trafił wyciągnie jeden z nich, będzie to zestaw klocków lego, pudełko puzzli lub szachy. Jeśli wyciągnie z worka dwa podarunki, może się zdarzyć pięć różnych układów prezentów. Jeśli wyciągnie z worka trzy prezenty, może się zdarzyć sześć różnych układów. Ile co najmniej sztuk prezentów znajduje się w worku Mikołaja?
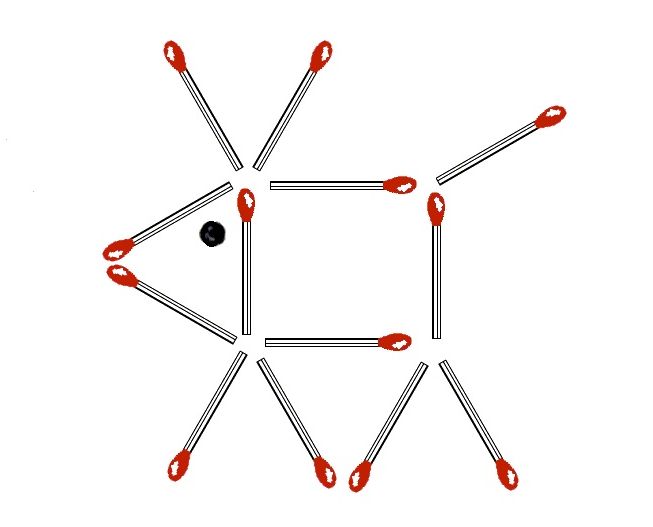
Zad. 2. Oto renifer Rudolf Czerwononosy zbudowany z zapałek i kamyczka. Jak przełożyć dwie zapałki i kamyczek, aby Rudolf patrzył w przeciwnym kierunku?
Zad. 3. Kierowca autobusu jadącego z Łamigłówkowa Dolnego do Łamigłówkowa Górnego ma na tę trasę przygotowanych 66 różnych rodzajów biletów. Na każdym bilecie podana jest nazwa przystanku początkowego i końcowego. Jaką maksymalną liczbę różnych biletów może sprzedać kierowca w czasie jednego kursu, jeżeli autobus mieści nie więcej niż 25 pasażerów?
Grudniowe zagadki nie sprawiły Łamigłówkowiczom trudności. Prawie wszyscy poradzili sobie z dwoma pierwszymi zadaniami. Punkty w zadaniu drugim przyznawaliśmy także za podanie innego niż firmowy sposobu przełożenia zapałek i kamyczka (Rudolf patrzył wtedy w drugą stronę, leżąc na plecach). Najtrudniejsza okazała się ostatnia zagadka, ale mimo to większość uczestników podała jej poprawne rozwiązanie.
Komplet 3 punktów zdobyli: Jacek Bagiński - nauczyciel matematyki z I LO z Krakowa, Mieszko Baszczak - uczeń SP 301 w Warszawie, Krzysztof Bednarek - uczeń III LO we Wrocławiu, Kamila Bojar - uczennica Zespołu Szkół Ponadgimnazjalnych w Szprotawie, Daria Bumażnik - uczennica II LO w Jeleniej Górze, Bartosz Czyżewski - uczeń I LO w Jeleniej Górze, Aleksandra Domagała - uczennica Gim nr 23 we Wrocławiu, Mateusz Jasiński - uczeń Zespołu Szkół nr 1 w Ostrzeszowie, Ewa Kaluś - uczennica I Społecznej Szkoły Podstawowej w Radomiu, Krystyna Lisiowska - redaktor z Warszawy, Bartosz Pawliczak - student II roku matematyki na PWr, Andrzej Piasecki - administrator IT z Oleśnicy, Tomasz Porębski - uczeń I LO w Krakowie, Jakub Ptak - uczeń SP 64 we Wrocławiu, Wojciech Sichniewicz - nauczyciel matematyki z Wrocławia, Tomasz Skalski - student matematyki na PWr, Adam Stachelek - uczeń SP 301 w Warszawie, Tomasz Stempniak - uczeń I LO w Ostrowie Wielkopolskim, Sabina Sy - studentka nanotechnologii na UJ, Jakub Tasiemski - uczeń I LO w Krakowie, Wojciech Tobiś - student automatyki i robotyki AGH, Wojciech Tomiczek - inżynier z Lipowej, Marzena Wąsiewicz - informatyk, a obecnie gospodyni domowa z Kajetan oraz Piotr Wróbel - inżynier sprzedaży z Brwinowa.
W Lidze Łamigłówkowej po trzech miesiącach czołowe miejsca zajmują:
- I m. - Krzysztof Bednarek, Daria Bumażnik, Aleksandra Domagała, Krystyna Lisiowska, Tomasz Porębski, Jakub Ptak, Wojciech Sichniewicz, Tomasz Skalski, Sabina Sy, Jakub Tasiemski, Wojciech Tobiś, Wojciech Tomiczek oraz Marzena Wąsiewicz (9 pkt na 9 możliwych),
- II m. - Jacek Bagiński, Mieszko Baszczak, Bartosz Czyżewski, Krzysztof Danielak - uczeń I LO w Jeleniej Górze, Bartosz Pawliczak, Andrzej Piasecki oraz Piotr Wróbel (8 pkt),
- III m. - Kamila Bojar (7,5 pkt),
- Tomasz Stempniak (7 pkt).
Wszystkim serdecznie gratulujemy!
Zad. 1. W worku Mikołaja jest co najmniej 6 prezentów: jeden pierwszego rodzaju, dwa drugiego rodzaju i co najmniej trzy trzeciego rodzaju.
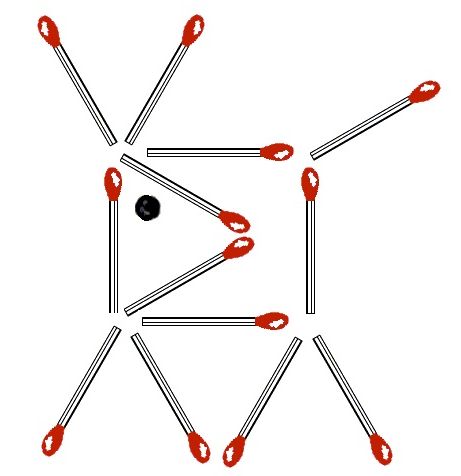
Zad. 2. Można zrobić to tak, jak na rysunku poniżej.
Zad. 3. Kierowca może sprzedać 55 biletów. Z treści wynika, że poza początkowym jest 11 przystanków, bo 1+2+...+11 = 66. Załóżmy, że na każdym przystanku czeka tylu pasażerów, ile biletów na trasy od tego przystanku ma kierowca. Gdyby autobus miał zabrać wszystkich czekających na przystankach, to między 6 a 7 przystankiem byłaby największa liczba pasażerów równa 36, czyli o 11 więcej niż jest miejsc. Z tego wynika, że może sprzedać nie więcej niż 55 biletów. Pokażemy, że te 55 biletów można sprzedać. Na 1. przystanku autobus zabiera 11 osób, na 2 jedna osoba wysiada, a wsiada 10 (w autobusie jest 20 osób), na 3 wysiadają 2 osoby i mogłoby wsiąść 9 oczekujących, ale zmieści się tylko 7, więc 2 bilety nie zostaną sprzedane (autobus jest pełny), na 4 wysiadają 3 i wsiadają 3 (5 pasażerów się nie zmieści), na 5 wysiadają 4 osoby i wsiadają 4 (3 pasażerów się nie zmieści), na 6 wysiada 5 pasażerów i 5 wsiada (1 osoba się nie zmieści), od 7 przystanku mieszczą się wszyscy czekający. Dodając liczby osób, które się nie zmieściły (i bilety dla nich nie zostały sprzedane), otrzymujemy 11, czyli 55 z 66 biletów wydano.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
