Zad. 1. Dany jest prostokąt o wierzchołkach (0, 0), (0, 2), (8, 0), (8, 2). Ile prostych przechodzi przez co najmniej 3 punkty kratowe należące do tego prostokąta? Punkty kratowe to punkty w układzie współrzędnych, których obie współrzędne są całkowite.
Zad. 2. W grupie 7 uczniów pewnego wrocławskiego liceum czterech jest rodowitymi wrocławiakami. Wiadomo, że:
- Jeśli Adam jest wrocławiakiem, to jest nim też Gerwazy.
- Jeśli Adam jest wrocławiakiem, to Franciszek nim nie jest.
- Jeśli wrocławiakiem jest Adam lub Dariusz, to nie jest nim Ernest.
- Jeśli Ernest nie jest wrocławiakiem, to Cezary też nim nie jest.
- Albo Bartosz nie jest wrocławiakiem, albo Dariusz nim jest.
- Albo Adam jest wrocławiakiem, albo Bartosz nim nie jest.
- Nie jest prawdą, że Darisz jest wrocławiakiem a Cezary nim nie jest.
- Wśród wrocławiaków jest uczeń, którego imię rozpoczyna się na literę G.
Którzy uczniowie to rodowici wrocławiacy?
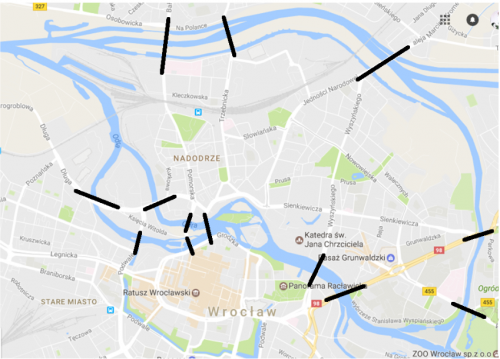
Zad. 3. W XVIII wieku szwajcarski matematyk Leonard Euler rozwiązał problem mostów królewieckich - pokazał, że nie można przejść po wszystkich mostach tego miasta dokładnie jeden raz. A jak to jest z układem mostów wrocławskich zaznaczonych na poniższej mapie kolorem czarnym?
a) Czy można odbyć spacer po Wrocławiu w taki sposób, aby przez każdy z tych mostów przejść jeden raz? Nie można przy tym korzystać z innych (niezaznaczonych) mostów.
b) Jeżeli zaznaczone mosty nie tworzą układu, który umożliwia taki spacer, uzupełnij mapę, dorysowując na niej jak najmniej mostów, by można było przejść po każdym moście czarnym i każdym nowym dokładnie raz. Ile jest dorysowanych mostów?
c) Czy (i jak) zmienią się odpowiedzi na powyższe pytania, jeśli dodatkowo wymagamy, by spacer zakończył się w tym samym miejscu, w którym się zaczął?
W tym miesiącu punkty otrzymali:
- 3 pkt. - Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr, Agnieszka Klich - informatyk z Wrocławia, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Andrzej Piasecki - administrator IT z Oleśnicy, Adrianna Tokarska - programistka z Krakowa, Tomasz Tomiczek - nauczyciel z Lipowej, Michał Węgrzyn SP 9 Wrocław, Gabriela Wołynko I LO Węgrów,
- 2,5 pkt. - Szymon Meyer - student matematyki na UWr, Dominik Zygmunt - student bankowości i finansów cyfrowych na UŁ.
Zad. 1. 44 proste.
Zad. 2. Cezary, Ernest, Franciszek, Gerwazy
Zad. 3. a) Tak. Plan miasta można przerysować w formie grafu (patrz rysunek poniżej), którego dwa wierzchołki mają rzedy nieparzyste (3 i 5), a pozostałe mają rzędy parzyste. Rząd wierzchołka to liczba wychodzących z niego krawędzi (mostów). Jeśli graf nie ma wierzchołków rzędu nieparzystego (nazywamy go eulerowskim), to spacer po jego krawędziach można odbyć, zaczynając od dowolnego wierzchołka i kończąc w tym samym wierzchołku. W jaki sposób taki spacer zaplanować? Jeśli graf ma dokładnie dwa wierzchołki rzędu nieparzystego (nazywamy go półeulerowskim), spacer po nim jest możliwy, jeśli zaczniemy go w jednym z nieparzystych wierzhołków, a skończymy w tym drugim. Możliwą trasę na ponizszym rysunku wskazuje porządek alfabetyczny. W innych przypadkach graf jest nieeulerowski i spacer po jego krawędziach nie jest możliwy.
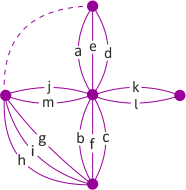
b) 0
c) Wystarczy dorysować 1 most łączący wierzchołki nieparzystych rzędów (linia przerywana). Za poprawną uznawano też odpowiedź 2, która jest skutkiem naturalnej interpretacji, że most nie przebiega przez duży obszar miasta.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
