czerwiec 2014

Zad. 1. Programista codziennie wkłada czystą koszulę flanelową w szkocką kratę. Co poniedziałek odwiedza pralnię, odbierając koszule czyste i zostawiając brudne. Ile koszul co najmniej posiada?

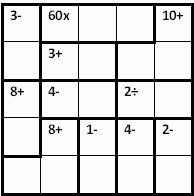
Zad. 2. Poniżej zamieszczono diagram kendoku 5×5. Zasady rozwiązywania tej łamigłówki są podobne do sudoku - każda cyfra od 1 do 5 powinna występować raz w każdej kolumnie i każdym wierszu. Ponadto liczby umieszczone w zaznaczonym obszarze po wykonaniu na nich zadanego w tym obszarze działania muszą dać podany dla tego obszaru wynik. Liczby w obszarze mogą się powtarzać. Oto przykład rozwiązanej łamigłówki.

Wypełnij pola poniższego diagramu cyframi od 1 do 5 zgodnie z zasadami kendoku. W odpowiedzi należy podać liczby wierszami.

Zad. 3. W czasie bitwy morskiej Rzymianie wzięli do niewoli 200 jeńców, którymi zamierzali zasilić rzymską flotę w charakterze galerników. Rzymski admirał lubiący łamigłówki postanowił jednak dać im szansę na uwolnienie. Zaplanował, że następnego dnia ustawią jeńców w rzędzie jeden za drugim, po czym nałożą im kapelusze w kolorze żółtym lub niebieskim. Każdy jeniec będzie widział tylko kapelusze stojących przed nim kolegów. Ci, którzy poprawnie wskażą kolor swojego kapelusza, zostaną uwolnieni, reszta trafi na galery. Rzymianie zaczną pytać o kolor kapelusza od ostatniego jeńca w rzędzie. Więzień może powiedzieć tylko: „niebieski” lub „żółty”. Pozostali usłyszą wszystkie odpowiedzi i wyroki. Jeńcy mają całą noc na przemyślenie strategii odpowiadania. Ile najwięcej osób i w jaki sposób mogą uwolnić?

Wyniki

W czerwcu wszyscy Łamigłówkowicze poprawnie rozwiązali diagram kendoku, a większość podała też poprawną odpowiedź do jednego z pozostałych zadań. Komplet punktów zdobyli: Jacek Bagiński, Krzysztof Bednarek, Daria Bumażnik, Krzysztof Danielak, Krystyna Lisiowska, Piotr Mazur, Bartosz Pawliczak, Andrzej Piasecki.

Była to ostatnia porcja łamigłówek w tym roku szkolnym. Zapraszamy do kontynuowania zabawy w październiku. Po raz drugi w historii Ligi najlepszemu zawodnikowi udało się rozwiązać poprawnie wszystkie zadania i zdobyć maksymalną liczbę punktów (miało to miejsce także w I edycji w roku szkolnym 2007/08). W czołówce Ligi Łamigłówkowej 2013/14 znaleźli się (w nawiasach podajemy zdobyte liczby punktów na 27 możliwych):

• (27 pkt) Jacek Bagiński – nauczyciel matematyki z Krakowa
• (25,5 pkt) Piotr Mazur – urzędnik ze Złotoryi
• ex aequo (25 pkt) Krzysztof Bednarek - uczeń III LO we Wrocławiu i Marzena Wąsiewicz - informatyk, a obecnie gospodyni domowa z Kajetan
• ex aequo (24 pkt) Krzysztof Danielak – uczeń I LO w Jeleniej Górze i Krystyna Lisiowska – redaktor z Warszawy
• (23,5 pkt) Andrzej Piasecki – administrator IT z Oleśnicy
• ex aequo (22,5 pkt) Daria Bumażnik – uczennica II LO w Jeleniej Górze i Bartosz Pawliczak – student matematyki na Politechnice Wr.
• (21 pkt) Kamila Bojar – uczennica Zespołu Szkół Ponadgimnazjalnych w Szprotawie
• (20,5 pkt) Wojciech Tomiczek – inżynier z Lipowej
• (20 pkt) Tomasz Skalski – student matematyki na Politechnice Wr.
• (19,5 pkt) Tomasz Stempniak – uczeń I LO w Ostrowie Wielkopolskim
• (19 pkt) Piotr Wróbel - inżynier z Brwinowa
• (18 pkt) Wojciech Tobiś – student automatyki i robotyki AGH Kraków
• (17,5 pkt) Mieszko Baszczak – uczeń SP 301 w Warszawie.

Wszystkim serdecznie gratulujemy!

Odpowiedzi

1. Programista ma 15 koszul. W poniedziałek 7 oddaje do pralni i 7 zabiera, a jedną ma na sobie.

2.

3. Można ocalić co najmniej 199 jeńców. Pierwszy odpytywany (ostatni w rzędzie) nie ma możliwości otrzymania jakiejkolwiek wskazówki. Zgadując, ma 50% szans na przeżycie. Pozostali mogą zostać uwolnieni, jeśli będą kierować się wcześniejszymi odpowiedziami. Wystarczy, że jeńcy umówią się, że pierwszy pytany odpowie 'niebieski', jeżeli zobaczy przed sobą parzystą liczbę kapeluszy niebieskich, albo 'żółty', gdy nieparzystą. Kolejny jeniec po usłyszeniu tej odpowiedzi porównuje ją z tym, co widzi przed sobą. Na tej podstawie wie, jaki ma kolor kapelusza i może poprawnie go określić. Każdy kolejny postępuje podobnie. Na podstawie usłyszanych odpowiedzi określa, jaka jest parzystość liczby niebieskich kapeluszy i porównuje z tym, co widzi przed sobą.