Zad. 1. Suma cyfr pewnej liczby dwucyfrowej A jest równa 11. Gdy A zwiększymy o 27, to otrzymamy liczbę, której cyfry będą zapisane w odwrotnej kolejności. Ile wynosi A?
Zad. 2. Ile jest liczb naturalnych trzycyfrowych podzielnych przez 13?
Zad. 3. Wykaż, że w trójkącie prostokątnym suma długości przyprostokątnych jest mniejsza od sumy długości przeciwprostokątnej i podwojonej długości wysokości opuszczonej z wierzchołka przy kącie prostym.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Konrad Andruchów - SP 4 Bolesławiec, Jakub Badowski - SP Mszczonów, Mieszko Baszczak - SP 301 Warszawa, Antoni Buraczewski - SP 107 Wrocław, Hubert Cabaj - SP Brzoza, Gracjan Ciupa - SP 72 Wrocław, Hubert Cymbalista - SP 1 Sobótka, Michał Gębarowski - SP Polna, Szymon Grech - NSP Koszarawa Bystra, Hubert Grześkowiak - SP Mieroszów, Natasza Henko - SP Mieroszów, Igor Hołowacz - SP Bielany Wrocławskie, Gabriela Kelner - SP Mieroszów, Marek Komorowski - SP 5 Żory, Natalia Krystkiewicz - KSP Mława, Martyna Kubiak - SP Skoki, Kacper Kuszaj - SP 2 Jelcz-Laskowice, Antoni Marczuk - SP 99 Wrocław, Zuzanna Prasek - SP Mieroszów, Jakub Ptak - SP 64 Wrocław, Mikołaj Roszczyk - SP 7 Legionowo, Kaja Srokosz - SP 52 Warszawa, Adam Stachelek - SP 301 Warszawa, Klaudia Sułkowska - SP Mieroszów, Bruno Szczepanek - SP Święta Katarzyna, Bartosz Szczerba - SP 35 Szczecin, Wiktor Szywała - SP 1 Sobótka, Michał Świerkowski - SP 215 Warszawa, Szymon Warmuła - SP Kobierzyce, Jerzy Wąsiewicz - SP Kostowiec i Aleksandra Zalewska - SP 1 Sokółka;
- 2,5 pkt. - Kacper Bernaciak - SP 30 Wrocław, Mikołaj Bilski - SP 6 Jelenia Góra, Norbert Frydrysiak - SP Mszczonów, Joachim Górski - SP Mszczonów, Szymon Kubiak - SP Skoki, Natasza Ptak - SP 118 Wrocław i Kacper Tylek - SP Świątniki Górne;
- 2 pkt. - Łukasz Banaś - SP 46 Wrocław, Antoni Bryszewski - SP 15 Jelenia Góra, Lena Bukowska - SP 1 Sobótka, Katarzyna Czarna - SP 1 Brzeg, Maja Frankowska - SP 3 Lubin, Malwina Górecka - SP 11 Inowrocław, Weronika Guzik - SP 1 Sobótka, Michał Kociszewski - SP 23 Wrocław, Jan Korbel - ZS Osiedle Niewiadów, Dawid Kramarczyk - SP 1 Brzeg, Kajetan Przybyła - SP ??? i Michalina Więckowska - SP 1 Konstancin-Jeziorna;
- 1,5 pkt. - Antoni Kołat - SP 45 Wrocław, Kajetan Pacześniak - SP 46 Wrocław i Gabriela Poświata - SSP 35 Legionowo;
- 1 pkt. - Mikołaj Cholewiński - SSP 35 Legionowo, Ewa Kaluś - SSP 1 Radom i Karol Raczkowski-Orleski - SP 45 Wrocław.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po czterech miesiącach Ligi Zadaniowej dla SP prowadzą: Gratulujemy!
Zad. 1. Liczba A to 47. Zauważmy, że liczby dwucyfrowe o sumie cyfr 11, które należy rozważyć, to 29, 38, 47 i 56, ponieważ większe od nich, tj. 65, 74, 83 i 92, mają cyfrę jedności mniejszą od cyfry dziesiątek, czyli po przestawieniu cyfr nie uzyskamy liczb większych. Łatwo sprawdzić, że spośród liczb 29, 38, 47 i 56 tylko 47 spełnia warunki zadania, bo 47+27=74.
Zad. 2. Takich liczb jest 69. Najmniejszą liczbą trzycyfrową podzielną przez 13 jest 104 = 13·8, a największą 988 = 13·76. Wszystkich liczb trzycyfrowych podzielnych przez 13 jest tyle, ile liczb od 8 do 76 włącznie, czyli 76-7 = 69.
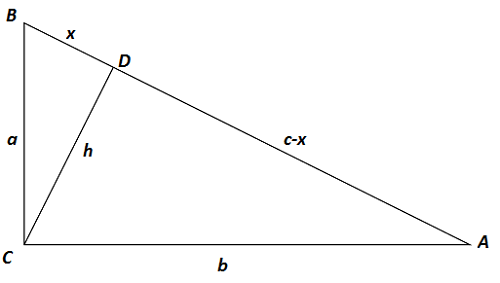
Zad. 3. W trójkącie prostokątnym ABC z kątem prostym w wierzchołku C oznaczmy: długości przyprostokątnych |AC|=b i |BC|=a, długość przeciwprostokątnej |AB|=c, długość wysokości opuszczonej z wierzchołka kąta prostego |CD|=h i długość odcinka |BD|=x. Z nierówności trójkąta otrzymujemy a < h+x oraz b < h+c-x. Po dodaniu tych nierówności stronami, otrzymamy a+b < h+x+h+c-x, a to po uproszczeniu daje a+b < 2h+c.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
