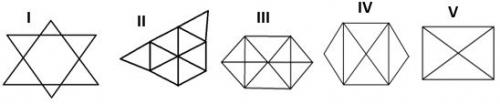
Zad. 1. Pinokio mówi, że narysował wszystkie poniższe rysunki bez odrywania ołówka od papieru i bez wielokrotnego rysowania tych samych linii. Jednak Pinokio dość często kłamie i nie można mu ufać. Czy są figury, których figur nie mógł w ten sposób narysować? Jeśli tak, to które?
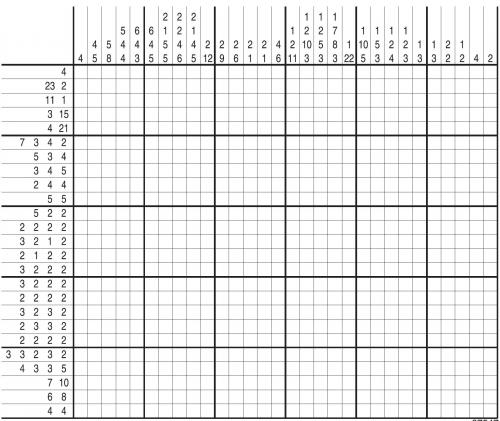
Zad. 2. Rozwiąż obrazek logiczny. W odpowiedzi napisz, co widzisz na tym obrazku.
Zasady rozwiązywania:
- w diagramie należy zamalować niektóre kratki,
- liczby w wierszach i kolumnach informują o tym, jakie grupy pól są w danym rzędzie zamalowane i w jakiej kolejności, między dwoma grupami zamalowanych pól musi być co najmniej jedna kratka niezamalowana.
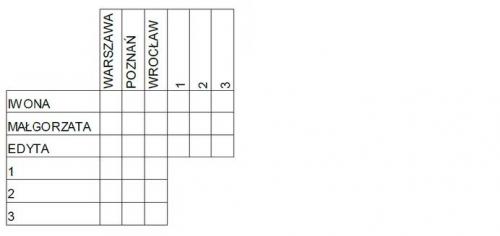
Zad. 3. Już 24 III 2019 rozegrany będzie w trzech miastach finał III Memoriału Urszuli Marciniak (czyli szkolnych mistrzostw w łamigłówkach). Każde z miast organizowało go inną liczbę razy. Na czele komitetu organizacyjnego w każdym mieście stoi kobieta. Na podstawie podanych informacji odpowiedz na pytania: Które z miast zainicjowało Memoriał, a które robi to po raz pierwszy? Kto jest odpowiedzialny za organizację finału w tych miastach?
- Iwona organizuje finał raz więcej niż pani z Poznania.
- Małgorzata nie pracuje w Warszawie.
- Rozgrywki odbędą się po raz drugi we Wrocławiu albo w Warszawie.
- Jeśli Iwona przygotowuje finał po raz drugi, to Edyta pracuje w Poznaniu. W przeciwnym razie Małgorzata robi to po raz pierwszy.
W marcu punkty zdobyli:
- 3 pkt: Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr, Joanna Janik - pracownik biurowy ze Stalowej Woli, Weronika Kiniorska - SP 118 Wrocław, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - urzędnik ze Złotoryi, Wiktoria Mróz - SP Wyrzysk, Julia Musiał - II LO Tczew, Andrzej Piasecki - administrator IT z Oleśnicy, Kamila Sobolewska - nauczycielka z Duninowa, Tomasz Tomiczek - nauczyciel z Lipowej, Michał Węgrzyn - SP 9 Wrocław,
- 2 pkt: Krzysztof Danielak - student automatyki i robotyki na PWr.
Zad. 1. Mógł narysować wszystkie poza V. Ta figura ma 4 punkty, w których schodzi się nieparzysta liczba linii. Pozostałe figury albo takich punktów nie mają (kreska, która wchodzi do danego punktu ma zawsze którędy wyjść) , albo mają takie punkty tylko dwa (jeden jest punktem startowym, a drugi końcowym).
Zad. 2. Grecka litera pi (małe) pisane kursywą. Patrz rysunek poniżej.
Zad. 3. Najwygodniejszym sposobem rozwiązania zadanie jest wypełnienie poniższego diagramu znakami + i - zgodnie z treścia zadania. W wyniku tego otrzymamy informację, ze Iwona organizuje konkurs po raz drugi w Warszawie, Małgorzata po raz trzeci we Wrocławiu, a Edyta po raz pierwszy w Poznaniu (co jest zreszta zgodne z prawdą).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
