Od stycznia 2014 zadania Ligi Zadaniowej dla Szkół Podstawowych należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Wyznacz ostatnią cyfrę liczby 20152014+20132012.
Zad. 2. Przez jaki czas w ciągu doby układ cyfr na zegarku elektronicznym wyświetlającym godziny i minuty w systemie 24-godzinnym wskazuje liczbę palindromiczną (czyli taką, która nie zmienia się czytana wprzód i wspak), w której liczby wskazujące godziny i minuty są jednocześnie liczbami pierwszymi?
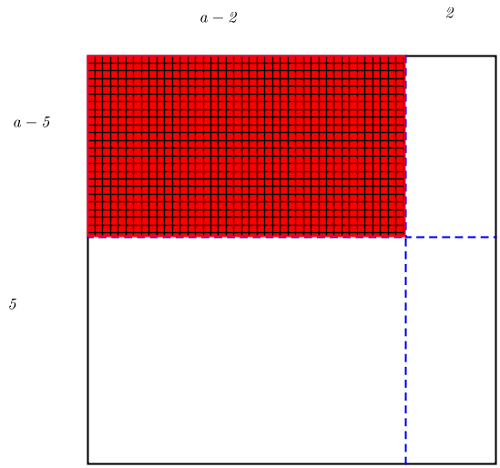
Zad. 3. Boki kwadratu zmniejszono odpowiednio o 2 cm i 5 cm. Otrzymany prostokąt ma pole mniejsze od pola wyjściowego kwadratu o 53 cm2. Oblicz długość boku kwadratu.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Zuzanna Banaś SP Bielany Wrocławskie, Ewa Blecha SP 26 Warszawa, Antoni Bryszewski SP 15 Jelenia Góra, Gracjan Ciupa SSP 72 Wrocław, Hubert Cymbalista SP 1 Sobótka, Jakub Dobrzański SP 3 Lubin, Marek Hajduk SP 9 Lubin, Michał Jerzak SP 103 Warszawa, Zuzanna Jóźków SP 1 Sobótka, Patrycja Karaś SP 15 Jelenia Góra, Nicoletta Litwin SP 15 Jelenia Góra, Zofia Ogonek SP 52 Warszawa, Magdalena Owczarek SSP Legionowo, Wojciech Pawłowski SP 63 Wrocław, Gabriela Poświata SP 35 Legionowo, Jakub Ptak SP 64 Wrocław, Mikołaj Roszczyk SP 7 Legionowo, Bartosz Szczerba SP 35 Szczecin i Wiktor Szywała SP 1 Sobótka,
- 2,5 pkt. - Natalia Hydzik SP 5 Słupsk, Marek Komorowski ZSP 5 Żory, Wojciech Piotrowski SP 150 Warszawa, Marcin Siemieński SP 52 Warszawa, Michał Tłuczek SP 10 Głogów i Adrianna Tomasik SP 2 Głuszyca,
- 2 pkt. - Mieszko Baszczak SP 301 Warszawa, Dominik Gąsior SP 52 Warszawa, Klaudia Jaczewska SP 52 Warszawa, Kamila Kwiatek SP Bielany Wrocławskie, Piotr Lara SP Świątniki Górne, Mateusz Milewski SP 1 Bogatynia, Olaf Olszewski SP 15 Jelenia Góra, Wiktoria Ratajska SP 15 Jelenia Góra, Aniela Reus SP 23 Wrocław, Amelia Szewc SP 1 Wołów i Michalina Więckowska SP 1 Konstancin-Jeziorna,
- 1,5 pkt. - Mateusz Lipiński SP 28 Wałbrzych,
- 1 pkt. - Mikołaj Cholewiński SP 35 Legionowo, Iwo Pilecki-Silva SP 76 Wrocław, Michał Piórkowski SP 63 Wrocław i Mateusz Winiarski SP 5 Krosno.
Pozostałym uczestnikom Ligi przyznano poniżej 1 punktu.
Po sześciu miesiącach Ligi z wynikiem 17,5 pkt. (na 18 możliwych!) prowadzi Zuzanna Banaś z SP w Bielanach Wrocławskich. Gratulujemy!
Zad. 1. Aby wyznaczyć ostatnią cyfrę sumy liczb, wystarczy znać ostatnie cyfry obu składników. Ostatnia cyfra iloczynu liczb zależy tylko od ostatniej cyfry czynników tego iloczynu (dlaczego?) zatem ostatnie cyfry liczb 20152014 i 20132012 są takie same jak ostatnie cyfry liczb 52014 i 32012. Wszystkie potęgi liczby 5 mają ostatnią cyfrę równą 5 (bo są to nieparzyste wielokrotności piątki). Ostatnie cyfry potęg trójki zmieniają się cyklicznie co 4 (dlaczego?) i są jedną z cyfr 3, 9, 7, 1. Liczba 2012 jest podzielna przez 4, zatem ostatnią cyfrą liczby 32012 jest 1. Po zsumowaniu ostatnią cyfrą liczby 20152014+20132012 jest 5+1 = 6.
Zad. 2. Wystarczy rozważyć liczby pierwsze nie przekraczające 24, bo podanie godziny jednoznacznie już określa liczbę minut w palindromie. W zapisie dwupolowym szukane liczby pierwsze to: 02, 03, 05, 07, 11, 13, 17, 19 i 23. Jednak trzy z nich można odrzucić, bo nie istnieją godziny 07:70, 17:71 i 19:91. W czterech kolejnych przypadkach liczba minut jest złożona: 02:20, 03:30, 05:50, 23:32 i tylko w pozostałych dwóch przypadkach otrzymujemy pierwsze liczby minut: 11:11 i 13:31. Zatem w ciągu doby zegarek elektroniczny wskazuje liczbę palindromiczną, w której liczby godzin i minut są jednocześnie pierwsze przez 2 minuty.
Zad. 3. Niech a oznacza szukaną długość boku kwadratu. Nowy prostokąt jest zaznaczony na rysunku kolorem czerwobym. Pozostałe 3 prostokąty mają razem pole równe 53 cm2. Pola tych prostokątów to (a-5)·2, (a-2)·5 i 5·2. Stąd 53 = (a-5)·2+(a-2)·5+5·2, czyli 53 = 2a-10+5a-10+10. Stąd 7a = 63, zatem a = 9 cm.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
