W tym miesiącu proponujemy łamigłówki primaaprilisowe. Gdzie tkwi błąd? A może go nie ma?
Zad. 1. Czy dodawanie jest łączne? Jeśli tak, to wartość sumy nie zależy od sposobu wstawienia do niej nawiasów. Tymczasem: 1−1+1−1+1−1+1−1+ … =
a) (1−1) + (1−1) + (1−1) + ⋯ = 0+0+0+⋯ = 0
b) 1 + (-1+1) + (-1+1) + (-1+1) + ⋯ = 1+0+0+⋯ = 1
Zad. 2. Rozprawa w sądzie zakończyła się w sobotę po południu następującym wyrokiem:
Skazany na powieszenie. Wyrok ma być wykonany w jednym z siedmiu dni najbliższego tygodnia. O dniu, w którym ma być wykonany wyrok, skazaniec dowie się rano w dniu egzekucji. Wcześniej o tym wiedzieć nie może. Czy ten wyrok może być wykonany?
a) Wyrok nie może być wykonany. Ostatnim dniem, kiedy można wykonać wyrok, jest niedziela. Gdyby jednak wykonać wyrok w niedzielę rano, więzień wiedziałby o tym już w sobotę po południu, czyli ostatnim dniem, kiedy można wykonać wyrok jest sobota. Gdyby jednak wykonać wyrok w sobotę rano, więzień wiedziałby o tym już w piątek po południu, czyli ostatnim dniem, kiedy można wykonać wyrok jest piątek. Kontynuując to rozumowanie, dochodzimy do wniosku, że wyroku nie można wykonać w żadnym dniu tygodnia.
b) Wyrok może być wykonany. Gdy wyrok został wykonany w środę, więzień, który przeprowadził wcześniej rozumowanie z punktu a, był tym terminem całkowicie zaskoczony.
Zad. 3. Istnieje na płaszczyźnie trójkąt, który ma dwa kąty proste.
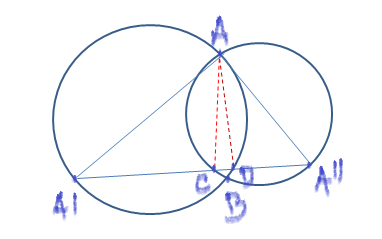
Niech dwa okręgi przecinają się w punktach A i B. Niech punkty A' i A" będą antypodyczne do punktu A na każdym z tych okręgów (tzn. A' i A" stanowią drugie końce średnic AA' i AA"). Połączmy punkty A' i A" odcinkiem, który przecina okręgi w punktach C i D. Poprowadźmy odcinki AC i AD. Kąt ACA" jest prosty, bo jest wpisany w okrąg i oparty na średnicy AA". Analogicznie prosty jest kąt ADA'. Wobec tego trójkąt ACD ma dwa kąty proste (w wierzchołkach C i D).
W tym miesiącu punkty zdobyli:
- 3 - Michał Węgrzyn ALO PWr,
- 2 - Bogusz Boliński I LO Kraków, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Igor Wojtun I LO Głogów,
- 1,75 - Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr, Tomasz Tomiczek - nauczyciel z Lipowej,
- 1,25 - Katarzyna Bęben I LO Kraków, Wojciech Mura - student matematyki na UJ, Andrzej Piasecki - administrator IT z Oleśnicy, Tomasz Smołka I LO Kraków,
- 1 - Agnieszka Klich - informatyk z Wrocławia,
- 0,25 - Krzysztof Danielak - student data science na UE we Wrocławiu.
Pozostali zawodnicy otrzymali 0 pkt.
Kwietniowe zadanią są przykładami sofizmatów, czyli rozumowań, w których ukryty jest błąd prowadzący do absurdalnego wyniku. Zadania te okazały się dla uczestników ligi dość trudne. Zgodnie z poleceniem należało wskazać błędy w podanych rozumowaniach, a nie przedstawić inne rozwiązanie problemu (np. stwierdzić, że ciąg sum częściowych szeregu naprzemiennego z jedynek nie jest zbieżny). Ponadto odpowiedzi zawodników często były mało precyzyjne i choć zbliżały się do sedna problemu, to go wyraźnie nie artykułowały. W tych wypadkach przyznawaliśmy punkty ułamkowe. Przepraszamy za oczywisty błąd w treści zadania 3 (pomylono punkty A' i A", co zostało już poprawione). Większość zawodników zwróciła na ten błąd uwagę, wielu innym nie przeszkodził on w poprawnym rozwiązaniu zadania.
Zad. 1. Dodawanie jest łączne, ale tylko wówczas, gdy dodajemy skończenie wiele składników. Nieskończone dodawanie nie jest dodawaniem i nie jest łączne (nie jest też przemienne, ani rozdzielne względem mnożenia, tzn. nie można wyłączyć wspólnego czynnika przed nawias).
Zad. 2. Rozumowanie w punkcie a) jest błędne. Rozpoczyna się od założenia „jeśli żyję w sobotę wieczorem”. Wynika z niego faktycznie, że w niedzielę wyrok nie może być wykonany. Dalsze rozumowanie jest jednak błędne, bowiem w dalszym ciągu wychodzi z założenia „jeśli żyję w sobotę wieczorem”, a w poprzednich dniach tygodnia nie wiadomo, czy założenie to jest spełnione. Jeśli założenie implikacji nie jest prawdziwe, to nie można wyciągać z niego żadnych logicznych wniosków.
Zad. 3. Punkty C i D pokrywają się, bowiem odcinek A'A" przechodzi przez punkt B (punkty A', B, A" są współiniowe, bo kąty A'BA i A"BA są proste i sumują się do kąta półpełnego).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
