Zad. 1. Wśród 21 monet jedna jest cięższa od pozostałych. Jak ją znaleźć za pomocą trzech ważeń na wadze szalkowej bez odważników?
Zad. 2. Ile jest liczb naturalnych mniejszych od 2016 i niepodzielnych ani przez 4, ani przez 10?
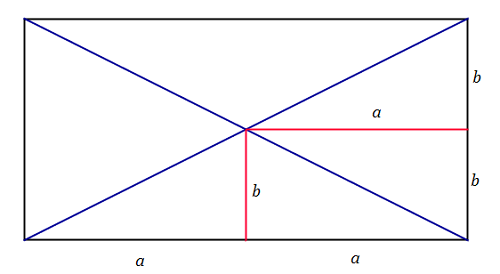
Zad. 3. W prostokącie różnica odległości punktu przecięcia przekątnych od jego dwóch sąsiednich boków wynosi 2 cm. Jakie są długości boków tego prostokąta, jeśli jego obwód ma 60 cm?
W tym miesiącu 3 pkt. zdobyli: Jakub Bartłomowicz SP 6 Jelenia Góra, Antoni Buraczewski SP 107 Wrocław, Kamil Faryński SP 11 Inowrocław, Marcin Faryński SP 11 Inowrocław, Maja Frankowska SP 3 Lubin, Malwina Górecka SP 11 Inowrocław, Szymon Grech NSP Koszarawa Bystra, Dariusz Marszałek SP 1 Brzeg, Krzysztof Możdżeń ZSP 5 Żory, Julia Pawicka SP Bielany Wrocławskie, Jakub Ptak SP 64 Wrocław, Antoni Skomorowski SP Bielany Wrocławskie, Marek Spychała SP 4 Warszawa, Kaja Srokosz SP 52 Warszawa, Adam Stachelek SP 301 Warszawa, Julia Szczechowicz SP 4 Mława, Bartosz Szczerba SP 35 Szczecin, Aleksandra Sznajder SP 4 Warszawa, Wojciech Szwarczyński SP Kowalowa, Jerzy Wąsiewicz SP Kostowiec, Jakub Wojnarowicz SP 2 Wrocław, Kacper Woszczek SP Mieroszów, Aleksandra Zakręcka SP 1 Mielec i Aleksandra Zalewska SP 1 Sokółka.
2,5 pkt. zdobyli: Joanna Gorajewska SP 2 Grodzisk Mazowiecki, Ewa Król SP Bielany Wrocławskie, Natalia Kstkiewicz KSP Mława, Tymoteusz Noremberg SP 2 Wrocław, Andrzej Nowak SP 2 Oborniki Śląskie, Dagmara Wroniszewska KSP Mława i Natalia Żądło SP 1 Mielec.
2 pkt. zdobyli: Mikołaj Bilski SP 6 Jelenia Góra, Nikola Busz SP Mieroszów, Nataniel Kędzierski SP 93 Wrocław, Antoni Kołat SP 45 Wrocław, Dominik Madejski SP 52 Warszawa i Michał Świerkowski SP 215 Warszawa.
1 pkt. zdobyli: Łukasz Banaś SP 46 Wrocław, Wiktor Sarnowicz SP 46 Wrocław i Jan Wiktorzak SP 23 Radom.
0,5 pkt. zdobyła Maja Zalewska SP 1 Kobyłka.
Pozostali uczestnicy otrzymali poniżej 0,5 punktu.
Po siedmiu miesiącach Ligi Zadaniowej z wynikiem 20,5 pkt. (na 21 możliwych) prowadzi Kaja Srokosz. Drugie miejsce z wynikiem 20 pkt. zajmują: Antoni Buraczewski, Maja Frankowska, Dariusz Marszałek, Julia Pawicka, Antoni Skomorowski, Bartosz Szczerba, Aleksandra Sznajder, Wojciech Szwarczyński, Michał Świerkowski i Jerzy Wąsiewicz. Trzecie miejsce z wynikiem 19,5 pkt. zajmują: Jakub Bartłomowicz, Mikołaj Bilski i Natalia Krystkiewicz. Gratulujemy!
Zad. 1. Jednym z rozwiązań możliwych jest podzielenie 21 monet na 3 grupy po 7 monet i zważenie dwóch dowolnie wybranych grup. Pozwoli to wyznaczyć, w której grupie siedmiu monet znajduje się moneta cięższa (wskaże to cięższa szalka, a jeśli będą w równowadze, to cięższa moneta znajduje się w grupie, która nie była ważona). Następnie wybraną siedmioelementową grupę monet dzielimy na trzy mniejsze grupy: dwie po 3 monety i jedną z 1 monetą. W drugim ważeniu na szalkach kładziemy grupy po 3 monety. Jeśli szalki będą w równowadze, to już po dwóch ważeniach wiemy, że cięższą monetą jest ta, która nie była ważona. Jeśli szalki się wychylą, wskażą grupę, w której jest cięższa moneta. Wówczas dwie monety z tej grupy kładziemy po raz trzeci na wadze. Jeśli otrzymamy stan równowagi, to cięższa jest moneta, która nie była ważona, a jeśli szalki się wychylą, cięższa jest moneta na niżej położonej szalce.
Zad. 2. Liczba zero jest podzielna przez 4, zatem nie ma wpływu na wynik, niezależnie od tego, czy zero uznamy za liczbę naturalną czy też nie. Liczb mniejszych od 2016 podzielnych przez 10 jest 201 (co dziesiąta), a podzielnych przez 4 jest 503 (co czwarta). Zauważmy, że co druga liczba podzielna przez 10 jest również podzielna przez 4. Takich liczb mniejszych od 2016 jest 100 (co dwudziesta liczba naturalna). Stąd liczb naturalnych mniejszych od 2016, które są niepodzielne zarówno przez 4 jak i przez 10, jest 2015–201–503+100 = 1411.
Zad. 3. Niech a i b oznaczają odległości punktu przecięcia przekątnych prostokąta od jego dwóch sąsiednich boków. Wówczas boki tego prostokąta mają długości 2a i 2b. Zachodzą równości a–b = 2 i 4a+4b = 60. Stąd a = b+2 oraz 4·(b+2)+4b = 60, czyli 2b=13 cm i 2a=17 cm.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
